I’ve tried to make mathematical discussions a much larger part of my class. Here’s what I’ve done.
The Protocols
To begin, my school is very protocol-driven. We use many of the protocols from the National School Reform Faculty, among others, along with protocols we create, tune, and share amongst ourselves. I use all kinds of protocols in class, including to run discussions. So these are what I’ve used this year.
Text-Based Seminar
For discussions based on texts, nothing beats the good old NSRF Text-Based Seminar. We use it often in Advisory (and for staff meetings). I used it toward the beginning of the year to discuss an excerpt from What’s Math Got to Do With It? (around page 40-41 if you’re interested…I don’t want to break any copyright laws). The trick as facilitator – as with any protocol – is to stick to the protocol, which in this case means holding learners accountable to referring to the text when speaking.
Pros: Keeps participants focused on the topic at hand without becoming a random opinion-spouting session.
Cons: This is a great protocol, but the opportunity to use it doesn’t come up all that much in my class.
Progress Fishbowl
This is a protocol I created based on a standard fishbowl when most of the class was struggling with a problem. I mean really struggling. A couple of groups in each class were finding some good solution paths and I wanted a way for them to share it productively. This one’s a bit lengthy – it could probably be pared in half.
Pros: Allows those with good ideas for solutions paths to help others without resorting to a “tutoring” situation. Those outside the fishbowl can come to their understanding through participation in the discussion rather than being told what to do.
Cons: It can get messy, particularly if some are totally lost. One time the protocol broke down entirely because the discussion was good enough on its own merits that a protocol was no longer needed. In that case, the class renamed it “the broken fishbowl”…we even drew a logo for it.
Linking Fishbowl
This protocol was my attempt to be sure all voices were heard. I’ve used it for conjectures on problems that were complex, yet had a low entry point. Most of the thinking is done beforehand, so it kind of amounts to a glorified share-out…until a learner pushes the previous speaker’s reasoning. Then it becomes glorious.
Pros: All voices are definitely heard, the discussion moves quickly, and it can go fantastically well when learners push each others’ thinking.
Cons: Since it is more of a share-out, learners can become disengaged once they’ve shared.
Yes, And… Protocol
My most recent creation, I used this for a similar reason as the Progress Fishbowl – to gather all the good ideas in one place and help those that needed it come to a better understanding. However, I wanted to avoid the breakdowns that can happen when disagreements occur, so learners had to build on what the previous speaker had said by prefacing with “Yes, and…” – which made for some great conversation. This went so well that it sparked me to write this post. I hardly had to say a word – my favorite kind of discussion!
Pros: All voices were heard, and great ideas were shared and improved upon.
Cons: It was actually fairly time-consuming. If you’ve got short class periods, it may not work for you (I have 90 minute periods, so I can pretty much do whatever I want).
What makes these kinds of discussions work? As a class and as a school, we focus on building a culture of trust, respect, and responsibility. We spend the first week-and-a-half of the school year exclusively on building culture – we don’t even touch content. Trust me, this pays off. Among other things, it creates the environment where these kinds of discussions are possible.
Also, it isn’t as if we do nothing but protocols. We have discussions everyday that are more typical of a classroom. But these are a great way to come to a wider understanding as a group for an important topic.
I’m leaving so much out; these protocols in a vacuum are worthless. But I thought they might spark some ideas for anyone looking for new ways to discuss mathematics in their classrooms.
Side note: I recently purchased Smith & Stein’s Five Practices for Orchestrating Productive Mathematics Discussions, but I also bought three other books at the same time (including the long version of A Mathematician’s Lament) so I haven’t even cracked it. That is to say that this post is a baseline of sorts; I want to get my thoughts and current strategies for discussions in writing before it all (probably) changes after reading Five Practices.
I just remembered that the main reason I created this blog was to post problems that I had been working on or thinking about…but apparently I forgot about that. So, finally, here is a new problem.
This was from last year and, because it’s very recognizable, I have decided not to use it again this year (I have a completely revamped problem ready to go, but don’t want to share too early…).
The problem was their introduction to right-triangle trig. The problem consisted of two documents. The first poses the problem, the second was created after the learners generated their need-to-knows. Of course, this is just the problem…the rest of the scaffolding, practice, protocols, etc. is not included because, well, that would mean I’d have to kill this blog because it’d take me too long to post.
First document: the problem scenario.
Second document: more information. (please excuse the stick man).
UPDATE April 12, 2013: Here is what I did this year instead…same idea, different picture. I liked it better.
First document: the problem scenario.
Second document: more information.
I’ve decided to follow Geoff’s lead, and help give the gift of Math Ed by listing some of my favorite blog posts from the past year. Geoff, and others in the comments, have listed some pretty solid posts, so I’m simply adding more.
Here goes, in no particular order:
- Bowman’s My 3 Favorite Whiteboarding Modes – this is the post that finally got me to take the trip to Lowes.
- David’s What if we gave them the answers? – I love any post that challenges my perspective on assessment.
- Bryan’s The Trouble With Assessment – same deal: any new perspective on assessment strikes a chord with me, and this pushed me to attempt my own version of portfolio assessments.
- Geoff’s We must get rid of Algebra because Roger C. Schank can’t behave at parties, knows weird mathematicians – this made me laugh surprisingly hard considering the fairly serious nature of the topic.
- Kate’s Hours of Entertainment – another reminder for me that there just might be a way to make anything fun.
- Michael’s White Paper on Problem Solving: The Why – I appreciated this series of posts, with the exception of the cats – I don’t like cats.
- Nat’s Bike Trail Task – I thought this was a cool idea, but the main reason I’m including it is because – and I might be wrong here – I think it was the first blog post I ever commented on.
- And although it’s not math-specific, I genuinely appreciated David’s The Best Thing; at the time, it really hit home.
There you have it. Happy Holidays.
Today I sucked.
Learners were not collaborating – instead they were sitting in groups, but working alone. I haven’t fostered collaboration well enough.
Learners were not taking risks – instead they were waiting to be told what to do, afraid to play around with the math. I haven’t encouraged risk-taking or designed problems that are open enough.
Learners were not having mathematical discussions – instead they were asking each other (and me) “how to do it.” I haven’t created an environment where learners are encouraged to converse in a mathematical fashion.
Learners were not taking pride in the quality of their work – instead they were doing it to get it done. I haven’t created a situation that made them want or need their work to be high quality.
Some of this is probably my own perception; today is the last day of the quarter, so the thought that runs through my head is that we’re a quarter of the way through the year, so they should be starting to get it…right?
But some of this is reality. I will reflect on my practices. I will change some strategies. I will implement some strategies that should have been in place from the start. I will not give up on things that I know will work in the long run. Today I sucked. But Monday I will be better.
Update: I was better Monday.
I was looking for a simple way to keep learners posted about their SBG progress. I like them (and me) to be able to see – at a glance – what concepts they have mastered and what they still need to work on. After tinkering a bit, I found a way to get Flubaroo to do it for me. I’d love to be able to do this in a more logical place like everyone else: their online gradebook. But I have to use a hybridized version of SBG because we don’t have school-wide SBG implementation (we’re unified in most everything we do, but I’m the only one currently pushing for SBG), and we grade a variety of school-wide learning outcomes. So I can’t directly use the gradebook for this. (For example, even though I label all of my assignments according to the concept, I still have to score them on a 10 point scale).
Anyway, here is what it can look like with Flubaroo. (If you aren’t familiar with Flubaroo, check it out…I hadn’t heard of it until a few days ago. But I can’t think of any reason that I would use it for its intended purpose).
- Create a dummy form in google docs with one “question” (actually, your first standard). Using a checkbox question, put in your options (I’m going with a binary “proficient” or “not yet”), and make sure to set it to record usernames.
- Open the spreadsheet. It’ll look like this:
- Add your students’ e-mail addresses below your submission (I copied and pasted from a .csv that I already had, so it took two seconds).
- Side-by-side with my gradebook, I enter whether the students are proficient or not with a single keystroke (once you’ve typed “proficient” or “not yet” once, a simple “p” or “n” will bring them up automatically).
- You can add more standards to the right of this column and repeat. When you’re done, have Flubaroo “grade” it.
6. This brings up a new tab with all your standards (with percentages and a pretty orange color if less than 70% of learners are proficient).
7. Finally, e-mail your students with a message.
The e-mail looks like such (which requires a little explanation to the learners…like the fact that it’s not a “grade”):
Why I like it:
- It gives me a clearer picture of how many learners are proficient on a given concept than my gradebook does. It also helps myself and our academic coaches when they are working with individual learners.
- The e-mail that it sends is very clear and color-coded – there should be no mistaking whether or not you are proficient on a concept.
- I didn’t have to write a script.
Why I don’t like it:
- It’s not the same as having it in the gradebook. For instance, the learners don’t have ready access at any time – they need me to e-mail it to them.
- It can only send an e-mail to everyone at once, with the same message. So for individual feedback it’s useless. Oh well, I’ll have to rely on my old standby: conversations with the kids.
- It uses misleading language (like “Your Grade”).
Other notes:
- You can easily modify this script if you’re into that sort of thing. For example, I found where to change the 70% cutoff…I could probably change the language too. But I bet I won’t.
- I know…I wish I could use a more pure form of SBG. But I get by.
Nope…that’s not a typo.
Almost every day I have moments where I think about how I teach now versus how I would have taught it several years ago. I definitely had one of those moments today.
I spent 20 minutes after school helping a learner understand that calculating the mean requires that we divide by how many numbers are in the set (his misconception was that we always divide by 2). It would have been soooo easy to simply tell this learner what to do – but I’m confident that it would have done little to help dispel the misconception and create a lasting understanding. So I took my time, tried several examples, and helped the learner see a pattern. In the end, I received one of teaching’s greatest gifts: the “Ohhhhhhhh, now I get it!” (Kudos to this learner, by the way, for persisting and not yelling at me to just give the answer). I have much more confidence that this learner has a deeper understanding and has overcome the misconception because, in a sense, he discovered it for himself.
On a related note, last year we spent a week working on measures of dispersion in an effort to become more adept at interpreting and using data. In the end, however, I felt like the learners still had no clue about the purpose of things like standard deviation. This year I wanted it to be different. I wanted them to understand why measures of dispersion are important and useful. I wanted them to discover this themselves. So I gave them sets of data that had the same mean, median, and mode, but had very different spreads. Then I asked them to “invent” a measure of spread – they even got to name it – so that we could better interpret the data.
We spent two days on this and they developed some interesting methods. Many of them were very similar to interquartile range, and a few were similar to standard deviation. We tuned and tested their measures with various data sets, and as an extension some groups were tasked with “breaking” their measure by finding a data set for which it did not work properly. It was a bit messy, but fun (for me, at least).
Tomorrow we begin a couple of days of studying established measures of dispersion. While they may not become experts, I have no doubt that they will better understand their purpose and use…because they have already discovered it for themselves.
Because I’m teaching the same classes as last year, I’ve been fired up all summer because I feel like I’ll be able to knock it out of the park. After two weeks of school-wide culture building, we finally began content this week. Regardless of whether I’ve taught the class before, I’ve never taught these classes – these kids. I have to start over. From scratch. Here’s some stuff I learned/remembered.
- It is a rough transition from passive to active learning – but it’s such a fun and important journey. I love the looks on learners’ faces after I walk away to another group. There’s this puzzled look that says “Wait…he didn’t answer our question. He only asked more questions. We have more thinking to do.” (At least that’s what I’d like to believe they’re thinking).
- Learners are used to being told what to do, step by step. This is made very clear the first time we determine our next steps. After being given a problem scenario, we determine what we know about the problem, what we need to know to solve it, and what our next steps will be. After the teeth-pulling required for Knows and Need-to-Knows this first time, we finally develop a solid list of next steps. The learners have created them, I have the learners repeat them, we have them listed on the board…but the first question I get after we begin working is “What are we supposed to be doing?” Their task is not laid before them, worksheet style with a list of things to do. Our next steps are aimed at tackling Need-to-Knows in whatever way best suits the learner. This is hard to wrap their minds around.
- Some habits – like hiding mistakes – are hard to break. As part of our cooperative environment, we have group contracts for each unit to help the groups work together. On this first contract, I included five problem-solving norms (mostly stolen from Malcom Swan) to get them started, but gave them the option to only use them if all members agreed. What I got was this:
Apparently rushing and erasing mistakes are important to kids.
Only about half the groups agreed to the norm for enjoying mistakes and not erasing work. I told them that’s fine…we’ll work on it.
- Adding the word “yet” to many learners’ comments makes a big difference. “We can’t figure this out”…yet. “Our group isn’t getting along”…yet. This leads us to determine our next move – how can we overcome this problem?
- Never carry a pencil. The beginning of the year is the most crucial time for this. By high school, kids have become very good (and stubborn) at getting you to do the work for them. Not carrying a pencil helps, but I have to remind myself not to carry a mental pencil either – to create a culture of questions rather than a culture of answers.
- At the end of the day, debrief. It took me until this year to figure this out, which is embarrassing. It’s as simple as holding three minutes sacred at the end of class (I build it into the agenda) to ask “what did we learn today?” or “what did you think of the day?” It gives learners the first opportunity to reflect on their learning, and I’ve already gotten some great insights from them.
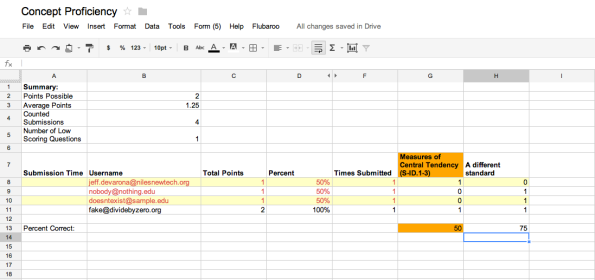
- Kids are more willing to believe “the internet” than a strong argument from peers. Sad face. This came about as we talked about measures of central tendency and particularly the mode. A problem was posed in which a data set had one of every number, but two 0’s and two 26’s. The question came up in every class – what is the mode? So I turned it back on them. What do you think? Let’s decide as a class. (Full disclosure: I don’t really know if the set should be considered bi-modal or if it has no mode…nor do I really care. The discussion that came from the question is more important to me than the answer). In one class, they came to consensus that the set had no mode, in another class they agreed to keep thinking about it…but in the third class, the following discussion occurred:
Learner 1: Since the mode is the most frequently occurring number, and there is a tie, then there is no most frequently occurring number. So there’s no mode.
Me: There’s an argument…anyone want to take the other side?
Learner 2: Well I looked it up and it said that both numbers were the mode – it’s bi-modal.
Me: What is “it”?
Learner 2: The internet.
Me: OK, so the “internet” said that this particular data set is bi-modal?
Learner 2: No, but it said that if there are two modes, then it’s bi-modal.
After a bit more discussion, we tried to come to consensus. The class agreed that the internet was right, and the learner’s solid argument was not.
So here’s another thing we’ll have to work on. And man am I fired up for this year – just not for the reasons I thought before the year started.
In general, I don’t like the Common Core State Standards (#standardizethat), but today I think I may have found a use for them.
I was looking for a student-friendly reading on what makes a good mathematics learner. My plan is to run a Socratic seminar prior to developing class norms and beginning our real mathematics work (we don’t start school until after Labor Day, and spent the first week and a half building school-wide culture…so we won’t even be starting “math” until Monday). I felt like my search was coming up short.
Then I remembered the Standards for Mathematical Practice within the CCSS. As it turns out, that part is not too bad – although it is a bit lacking on some things I consider important, like learning from mistakes and risk-taking.
I re-phrased, re-worded, and deleted my way to what I think will be a decent, short read for learners leading into a text-based seminar. Here it is…I’d love to hear what you think (is it still over a ninth-grader’s head? will it help spark meaningful discussion? is it just garbage warmed over?).
(the formatting is a little screwy…I think because I wrote it in Pages).
As part of the Math Blogger Initiation Project, Sam Shah, in his classic avuncular style, offered us the prompt to share anything that we are proud of. Wait – of which we are proud. Whatever. Anyway, I’ve decided to share the very first random problem idea that I ever had. Here it is – pay no attention to the horrid diagram, not to mention the ridiculous context. (And here’s the google doc version, which is where all my work resides).
This was an introductory problem to a unit on circles, and the goal was simply to review basic concepts like radius, diameter, circumference, and area of a circle. It is by no means the greatest problem, and it would be vainglorious to claim it as such. However, I am proud of it for this reason: it marked a personal turning point for when I finally started to “get it.”
I mean “get it” in two ways. First, I realized that it is far better to create your own problems than to steal them wholesale. Believe me, I am not creative and I spend a great deal of time taking Henry Wong’s advice to beg, borrow, and steal. I steal a ton of ideas from all over – colleagues, the interwebs, books, strange cloud formations…but there are some things that are so much better if you create them yourself. And problem ideas are one of those things. (To avoid turning this into a white paper, I think another post may be in order for this topic).
Second, I started to understand what it takes to make a good problem – things like multiple entry points that are accessible to all learners, multiple solution paths, allows opportunities for extension, etc. If I could take a mundane review topic and create a decent problem out of it…well I can do anything, right? And the thing is, the problem is almost Hemingway-esque in its simplicity. I mean, there’s not much to it…and there doesn’t need to be. (By the way, if you’ve never read Hemingway’s “Cat in the Rain”, do it. It takes all of three minutes and is the best short story of all time according to this math teacher).
Since that time, my mind has shifted to be on a constant quest for problem ideas. Most of them hit me at the most inopportune times…which means just at the moment that I’m about to fall asleep. At first it was kind of a rare occurrence, but now I see them all over the place: the label on a bottle of Mountain Dew, some fried okra, a dirty windshield. Not to sound trite, but math really is everywhere…especially when you’re on the lookout for random problem ideas.
Every year I make two or three personal teaching goals for the coming year…but I never write them down and I rarely tell anyone. This year I have told many people, and I have more than a few goals – eight in all! Some of them are new for me and some of them are simply a desire to continue what I’ve been doing, but do it better. Still others I could really use some help with, so I’d love any feedback.
Here goes:
1. Step up my SBG game
Last year I tried my best to implement at least a version of Standards-Based Grading. It certainly wasn’t “pure” SBAR, although I don’t think that I want it to be. I gave a presentation at New Tech’s Annual Conference about how we graded and ended up learning a lot from other teachers (go figure). One element I want to add this year for skills assessments is a simple rubric at the top (or bottom) of the quiz that lets learners know up front what will be considered “Proficient”. Last year I made the determination about what “Proficient” meant after the quiz was already done. Big mistake.
[Update: It didn’t take long to get more info on this one. The same day I posted it, I found this post from Dan Bowdoin…between his post itself and the plethora of links, I think I’ve got exactly what I need.]
2. Improved questioning and mathematical discourse
This is a repeat goal for me. How I interact with learners and the environment that we set up as a class for mathematical discussion has always been important to me, but boy do I need a lot of improvement. An eye-opener for me prior to last year was watching this video of Deborah Ball, dean of the School of Education at the University of Michigan, teaching a group of fifth grade students (scroll down to the BlueStream button). The eye-opener: never once does she say that an answer is right or wrong…she just facilitates the discussion so that the students make that determination. Recently, I came across David Cox’s post on Creating a Culture of Questions and was amazed at how similar his description was to how I tried my best to run class last year. If anyone has other suggestions for resources on this kind of thing, particularly facilitating mathematical discourse, I would love to hear from you.
3. Continue having learners create tutorial videos
Last year we received some grants to have learners create tutorial videos (similar to Khan Academy only in the sense that they are videos – the value was in their creation, not their use). I saw many benefits in this process, but I made soooo many mistakes in its implementation. In fact, I have yet to upload any videos because I’m still deciding if I should – here is where they would go. The problem: I did not build in enough time for drafting, revision, reflection, and checkpoints. In other words, the final products ended up so full of mistakes that I may not be able to post them at all. Big lesson learned.
4. Provide a video alternative to practice (aka homework)
As I reflected on what went wrong with the tutorial videos, I thought that it would have helped if I’d had groups create a simple video of themselves explaining the concept on a whiteboard. Then I thought, why not do that for a regular assignment? I (and the learners) could get way more information about their understanding and their misconceptions from them explaining a single problem than I could from seeing thirty problems they’ve done on paper. The only issue is I haven’t worked out exactly how to do it. We have mini-whiteboards, and every learner has a laptop with a webcam…suggestions???
(As a side note, I’d be remiss not to mention that I don’t give homework very often, and only after its purpose is clear. Just saying.)
5. Give feedback in a more timely manner
Another repeat goal. I’ve got to get quicker at giving feedback to learners…I’m talking same day or next day. The value of it can’t be overstated. I think I’ll be able to do a better job this year; last year we were creating a new school – year two will be easier…right?
6. Continue to celebrate mistakes
I try to create an environment where it’s understood that we are all learning together, and that mistakes are another tool to help us learn. Last year after handing back a practice assignment, we would celebrate our “favorite wrong answer” – an idea that I stole from Leah Alcala’s “My Favorite No”.
I also love the idea behind Michael Pershan’s page, Math Mistakes, and he also tweeted this over the summer:
I haven’t figured out the logistics yet, but I’d love to do this in my math class one way or another. Again, any suggestions would be awesome.
7. Math Whiteboarding!
Having followed Frank Noschese’s blog, I’ve been interested in using whiteboards more effectively…but it didn’t make it onto my plate last year. But now I’ve seen how Bowman Dickson has used whiteboarding for math, and Kelly O’Shea’s mistake game sounds fantastic. I can’t wait to try these out.
8. Incorporate more student passion into my class
As I found out through writing and reflecting on this post on passions, this is not so easy. But I think I’ve got some good ideas…we’ll see what happens.
So there you have it. I’ll definitely update as the year progresses…
The Problem Bank 